Théorème de Pythagore & sa réciproque : formule et exemples

Le théorème de Pythagore est un théorème de géométrie, étudié au collège en France. Il est nommé d’après le philosophe de culture grecque du VIe siècle av. J.-C. Pythagore (Puthagóras, Πυθαγόρας en grec) qui, sans l’avoir découvert, l’aurait formalisé pour la première fois. Plutôt que Pythagore, c’est peut-être son école et ses disciples, installés au sud de la péninsule italienne (dominée à l’époque par la culture grecque, si bien qu’elle était nommée la Grande Grèce), qui ont formalisé ce théorème.

Théorème de Pythagore : formule

Selon le théorème de Pythagore : dans un triangle rectangle, le carré de la longueur de l’hypoténuse est égal à la somme des carrés des deux autres côtés. 

Le théorème de Pythagore s’applique aux triangles rectangles uniquement.

• Un triangle rectangle est un triangle qui compte un angle droit, c’est-à-dire un angle de 90°.
• Le carré consiste à multiplier un élément par lui-même. Il est noté avec l’exposant « ² ». Le carré de 2, 2², correspond donc à « 2 × 2 », donc 4.
• L’hypoténuse, du grec upoteinousa, ὑποτείνουσα (littéralement « tenu au-dessous »), désigne le côté du triangle qui fait face à l’angle l’angle droit. C’est aussi le côté le plus long du triangle. Les deux autres côtés sont parfois nommés les « cathètes ».

Pour un triangle rectangle ABC, rectangle en A, le théorème de Pythagore se traduit par la formule :

BC² = AB² + AC²

Exemple avec le théorème de Pythagore

Soit un triangle ABC rectangle en A. On connaît les longueurs des côtés de ce triangle.

AB = 3 cm
AC = 4 cm
BC = 5 cm

BC est l’hypoténuse.

Selon le théorème de Pythagore, le carré de l’hypoténuse de ce triangle, BC, doit être égal à la somme des carrés des deux autres côtés, AB et AC. Donc :

BC² = AB² + AC²
5² = 3² + 4²
5×5 = 3×3 + 4×4
25 = 9 + 16
25 = 25

Le théorème est vérifié, BC² est bien égal à AB² + AC².

Calculer une longueur avec le théorème de Pythagore

L’égalité présentée par le théorème de Pythagore nous permet de calculer une longueur, qui nous est inconnue, lorsque l’on connaît les deux autres longueurs.

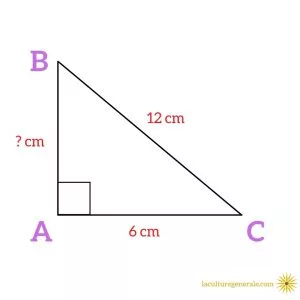
Soit un triangle ABC rectangle en A. BC est l’hypoténuse. On connaît deux longueurs de ce triangle.

BC = 12 cm
AC = 6 cm

Quelle est la longueur de AB ?

BC² = AB² + AC²
12² = AB² + 6²
144 = AB² + 36
144 – 36 = AB²
108 = AB²
√108 = AB
AB ≈ 10,39

La longueur AB est à peu près égale à 10,39 cm. C’est une valeur approchée : en effet, la racine carrée, notée ci-dessus « √ », nous a donné une valeur complexe, avec de nombreuses décimales (10,3923048454).